前言

根据量子力学的特性进行编码和信息传输的信息处理方式使得量子通信理论上实现无条件安全，量子设备是量子信息处理中不可或缺的元件。

在设备无关的量子态认证中，关于两体纠缠态的自测试结果己经很丰富了，但是对于多体量子态的研究在最近几年才刚刚开始。文章源自千电号-http://www.xmxqx.com/46404.html

任意两量子比特的纯态存在一种标准的施密特分解，只由一个参数确定，由于多体量子态形式的多样性，其自测试方案相比于两体纠缠态要复杂很多。文章源自千电号-http://www.xmxqx.com/46404.html

在目前的多体纠缠态的自测试方案中，无论是基于特殊观测量的统计值，还是基于Bell不等式的违背值方案都涉及全部方的联合概率统计。文章源自千电号-http://www.xmxqx.com/46404.html

在本文中，提出了在设备无关的领域中，利用边际信息认证多体态的思想和方法，通过N-1方的关联关系实现几类不同的N方纠缠态的自测试，从而可以达到量子态层析的效果，此外，本文的方法可以推广到参与方N≥3的量子态中。文章源自千电号-http://www.xmxqx.com/46404.html

凸集上不同类型的点定义

—个空间上的集合C包含于Rn是凸集的条件是，如果存在集合Ｃ上的两个点x1，x2∈Ｃ，它也包含着这两个点之间的连线：文章源自千电号-http://www.xmxqx.com/46404.html

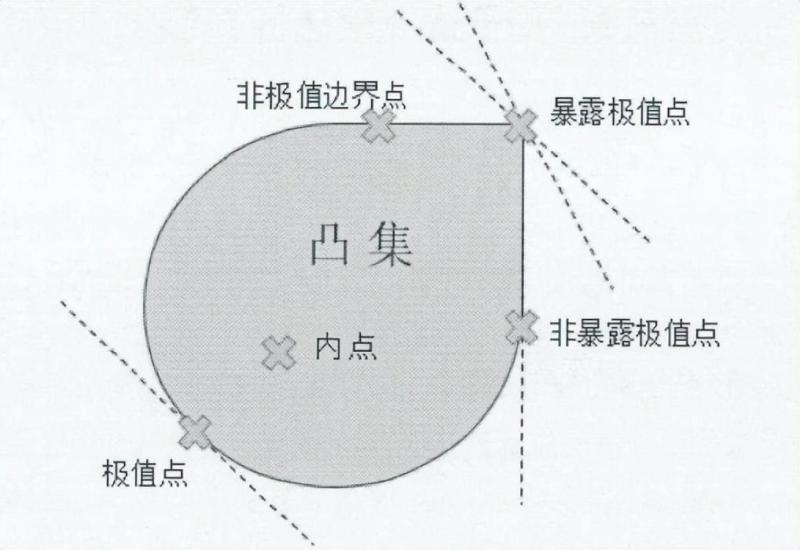
从几何角度分析，一个有界的凸集有几种不同类型的点组成，包括边界点和内点，边界点又可以细分为极值点、暴露点、非极值边界点和非暴露极值点。文章源自千电号-http://www.xmxqx.com/46404.html

边界点指集合面上的点，记为Cbnd,极值点是某些边界点不能由其他边界点的线性组合表示的点，记为Cext，暴露点是极值点中存在不同的切线的点，记为Cexp，从集合的包含关系来说，Cext包含于Cexp包含于Cbnd。文章源自千电号-http://www.xmxqx.com/46404.html

基于全概率的W态的自测试

2014年，Wu等人首次提出了W态的自测试方案，在此方案中，研究者提出了将三量子比特系统投影到两维的量子比特空间，然后基于两体纠缠态的自测试方案实现整体态的自测试思想。文章源自千电号-http://www.xmxqx.com/46404.html

这一思想的提出对三体以上纠缠态的自测试具有重要的启发，2018年，将其应用到了任意N≥3时W态和GHZ态的自测试方案中。文章源自千电号-http://www.xmxqx.com/46404.html

如果Alice、Bob和Charlie三方共享一个未知的量子态|Ψ>，每方各自执行三个未知的测量，且每个测量各有两个不同的输出结果，并有如下测量结果成立：文章源自千电号-http://www.xmxqx.com/46404.html

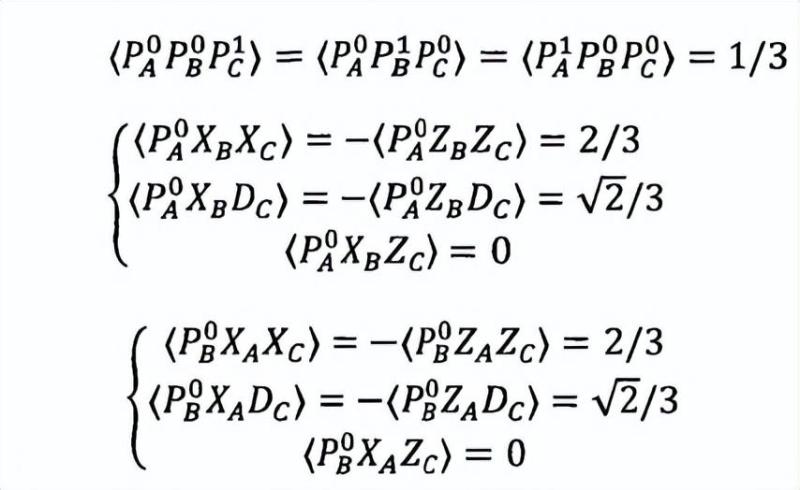
其中P0=PZ=+1=（I+Z）/2以及P0=PZ=-1=（I-Z）/2是不可信测量Ｚ的投影，那么设备中未知的量子态与W态局域酉等价。文章源自千电号-http://www.xmxqx.com/46404.html

2014年，Miguel等人根据W态的对称性，研究了每方持有两个未知的测量算子，通过构造Bell不等式的方法实现自测试的方案。文章源自千电号-http://www.xmxqx.com/46404.html

由于W态属于2×2×2的希尔伯特空间且三方系统具有对称性，因此每方的测量可以考虑在X-Z平面，并由泡利算子σZ和σx之间的夹角φ1和φ2确定：文章源自千电号-http://www.xmxqx.com/46404.html

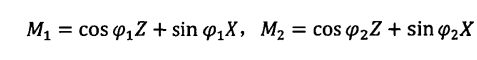
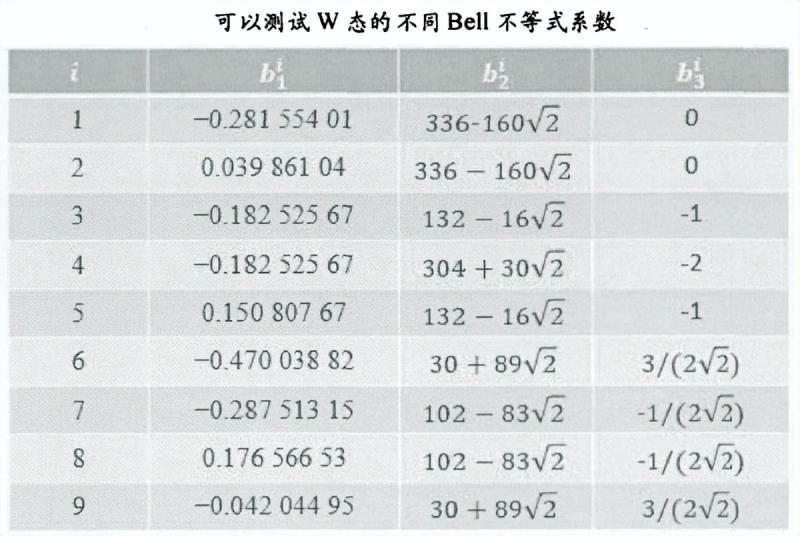
为了找到合适的Bell算子，充分利用所有的概率统计，因此构造的Bell不等式中包括以下９组不同形式的测量期望值。文章源自千电号-http://www.xmxqx.com/46404.html

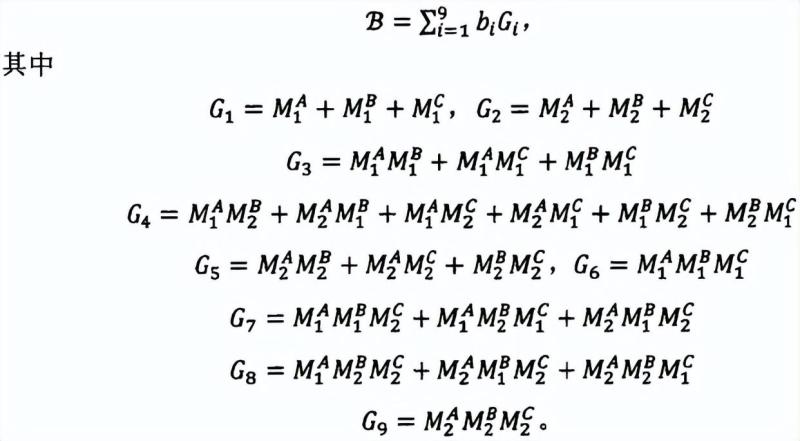
为了使得W态是所构造算子的最大特征值对应的特征向量，每组测量作用在W态后的量子态得到的系数需满足两点，W态中存在的项|001>，|010>和|100>三项系数相等，其他５组项的系数需等于零。文章源自千电号-http://www.xmxqx.com/46404.html

从而求解关于系数的线性方程组，在有效的解空间内，测量角度的参数和Bell不等式的系数构成的特征值应为最大值。文章源自千电号-http://www.xmxqx.com/46404.html

基于边际信息期望值的自测试

在量子态层析的任务中，通常人们可以利用可信的测量，通过重复的实验所得到的实验期望值，来重构设备中量子态的约化密度矩阵，其中3-qubit的W态是纯态的一个例子。文章源自千电号-http://www.xmxqx.com/46404.html

由于W态特殊的对称性和纠缠性，它取偏迹之后的子系统依然是一个纠缠态，而且具有一定的对称性，考虑一个被纯化后的辅助量子系统Ｘ，因为Ｂ系统是一个量子比特，假设|E2>和|E2>，则：文章源自千电号-http://www.xmxqx.com/46404.html

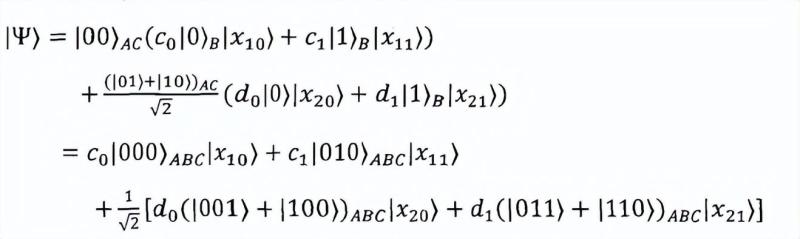
为了方便，将密度算子ρAB展开，综上可知：文章源自千电号-http://www.xmxqx.com/46404.html

给定两体AB和AC的部分信息，整体的W态的密度矩阵就可以被重构，给出几类不同利用边际信息期望值自测试三量子比特纠缠态，不但给出了观测结果完美情况时设备中未知态和目标态的保真度，并结合鲁棒性进行了分析。文章源自千电号-http://www.xmxqx.com/46404.html

实验方A、B和C三方各有三个测量，分别标记为X，Z和D，输出结果记为±1，如果一方和两方的测量概率结果满足如下关联值：

局域同构等价，而且这个自测试方案是具有鲁棒性的，事实上，这些概率期望理想情况下是W态测量得到，测试W态相同的局域同构线路图，如下图所示。

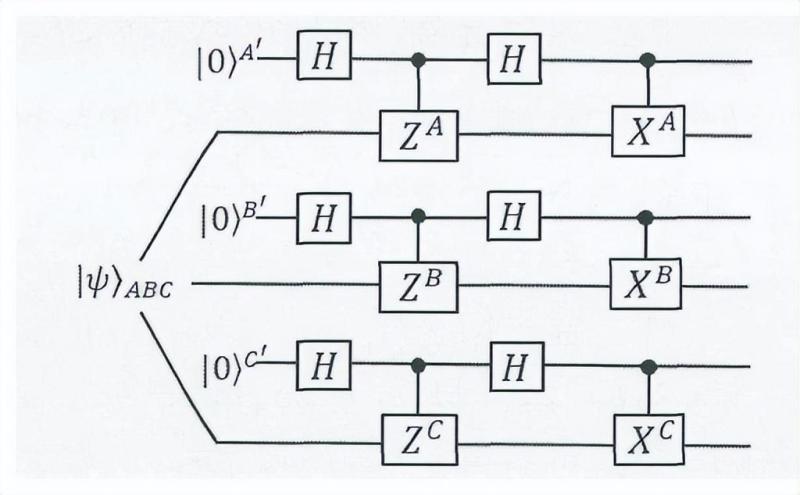
注意的是局域同构线路只是在解析分析中提取保真度函数的一个数学过程，并不需要在实验过程中真正的搭建，因此，在真正的实验过程中，唯一要做的仅仅是统计测量结果。

由于W态的对称性，每方测量形式也是完全相同的，对称性也会反应在swap线路、约束条件和目标函数中，我们为了减少NPA矩阵中的变量，引入群论中的对称变换，将G中的６个函数同时作用在NPA矩阵行和列中，然后取均值重新生成的NPA矩阵是实际运行的矩阵。

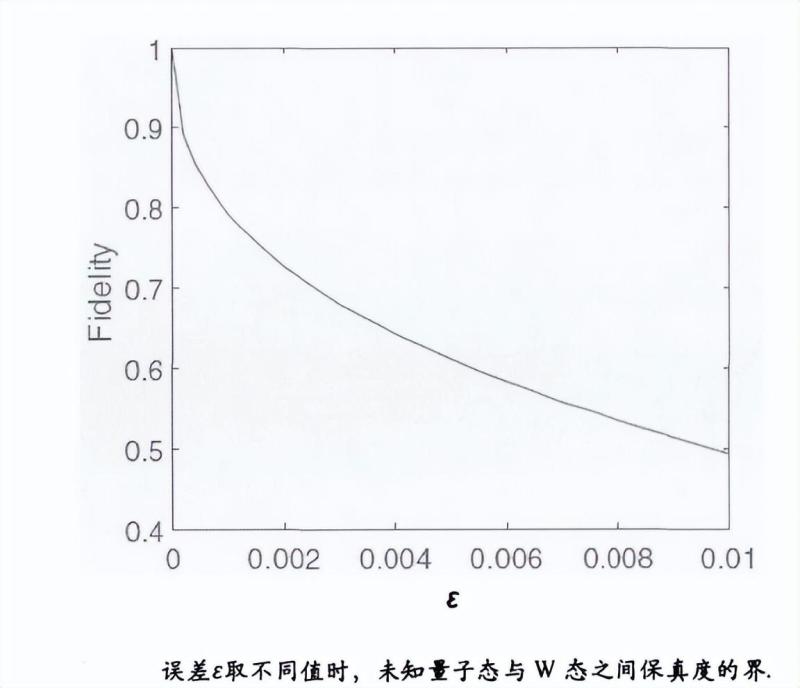
在实验过程中，设备内部的噪声和统计的误差是不可避免的，这些误差对自测试结果也有存在一定影响，为了探究通过这些概率分布得到的自测试结果，我们考虑白噪声，在理想概率值上乘以1-ε，此时待解决SDP问题中的NPA矩阵可以表示为：

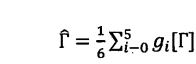
需要注意的是虽然每方的第三个测量Ｄ并没有出现在swap线路图中，但是它对约束保真度的界有重要的作用。

此外，我们可以根据两方的关联得到部分整体的观测量的结果，此关联关系对整个系统具有轮转对称性。

从半正定规划问题的对偶问题可知当ε＝０时，我们可以提取一个每方三个测量，每个测量有两个输出的轮转对称的不等式B。

这个不等式的最大违背值可以通过统计测量结果得到，不等式的通项可表示为：

从以上对偶问题提取的不等式系数中可以发现α≈-λ0，而且其他的系数都是非常小的数，可以猜测其解析形式为Β≈S0-T00，此时可以认为关联实际上量子集上的一个非暴露极值点，也就是说这组关联关系不可以构成一个有效的Bell不等式。

为了证明这个猜测，我们构造了关联关系中在非超光速集合中的一个切面，如下图所示。

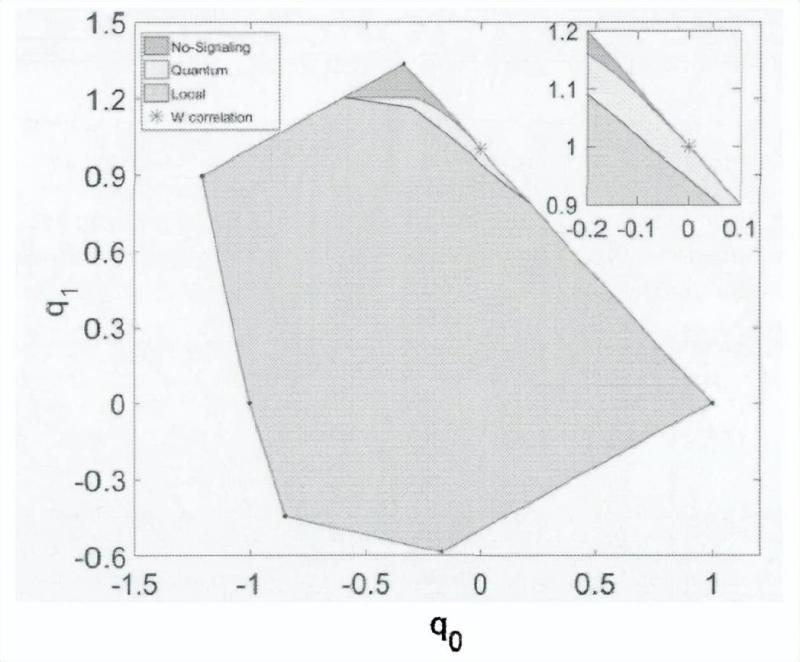
经过量子关联在量子集的位置的切线可以被经典策略实现，因此不存在一个有效的Bell不等式，使得它可以比经典集合更有优势，即在只有关联的条件下，只能通过极值点对W态测试。

广义Ｗ态的自测试

除了标准的W的态，给出一类广义的Ｗ态在边际条件下的自测试方案，一类函数的3-qubit纠缠态的自测试方案。

Alice、Bob和Charlie三方共享一个量子系统，每方拥有一个含有两个输入的测量设备，记为A0，A1，B0，B1，C0，C1，如果关于测量的统计结果满足如下关系，那么设备中的态与目标态局域酉等价。

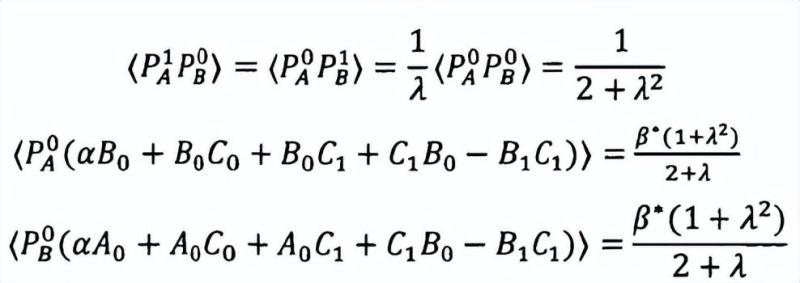
主要思路是Alice、Bob和Charlie其中一方用不可信的投影测量将剩下的两个系统的投影到其子空间中，然后子空间中的两体纠缠态可以根据部分纠缠态的自测试方案不等式的最大违背值实现自测试。

但是这样的方案依然需要统计三方的联合概率，我们将尝试利用一方和两方的联合概率实现目标态的自测试。

对任给的参数λ∈（0,1]，如果－方和两方的统计结果满足，那么三量子比特的纠缠态可以实现自测试，而且结果具有鲁棒性，我们每方用（X，Z，D）表示三个不可信的测量，根据目标态的对称性，关联关系分为三组：

集合１，对A和B两方，任意的m，n={A，B}且m≠n：

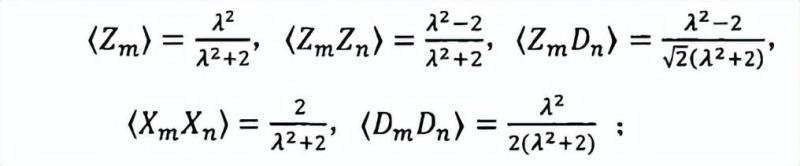
集合２，对A和B中二者之一和C，任意的ｍ∈{A，B}：

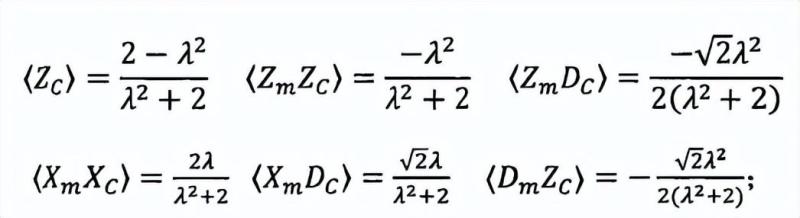
集合3，对A、B和C三方中的任意两方，既ｍ，n∈{A，B，C}，且m≠n：

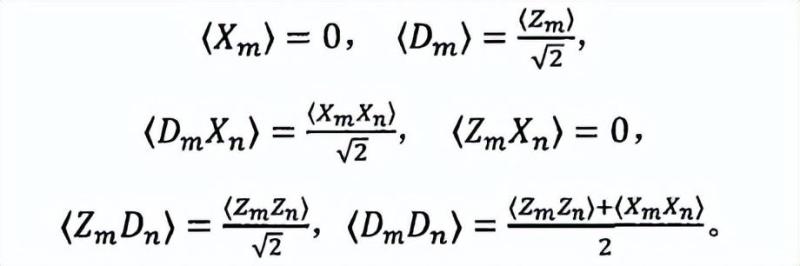
构造同构映射的方法与W态类似，保真度可以写成是观测结果和变量的线性函数，此时保真度依赖参数λ，但是目标态并不像W态三方具有完美的对称性，因此这里的半正定规划算法能不附加群对称性质，如下：

生成的NPA矩阵，维度是83×83的，如下图所示，保真度的值f＞99.8%，这个结果离１的差距是由NPA层数约束条件过松导致的。

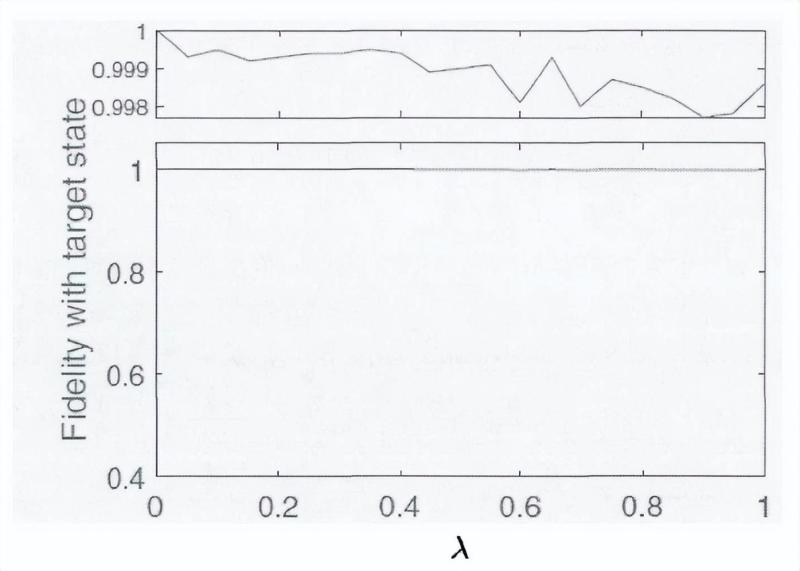
当λ=０时，为一个可分态而不再是纠缠态，保真度会高于其他点，此外我们还研宄了N=4时的W态的自测试：

与上述两种态相同，这里每方依然使用（X，Z，D）三个测量，并统计三方的概率分布，如果测量结果满足相关的统计值，那么设备中的未知量子态与目标态局域等价。

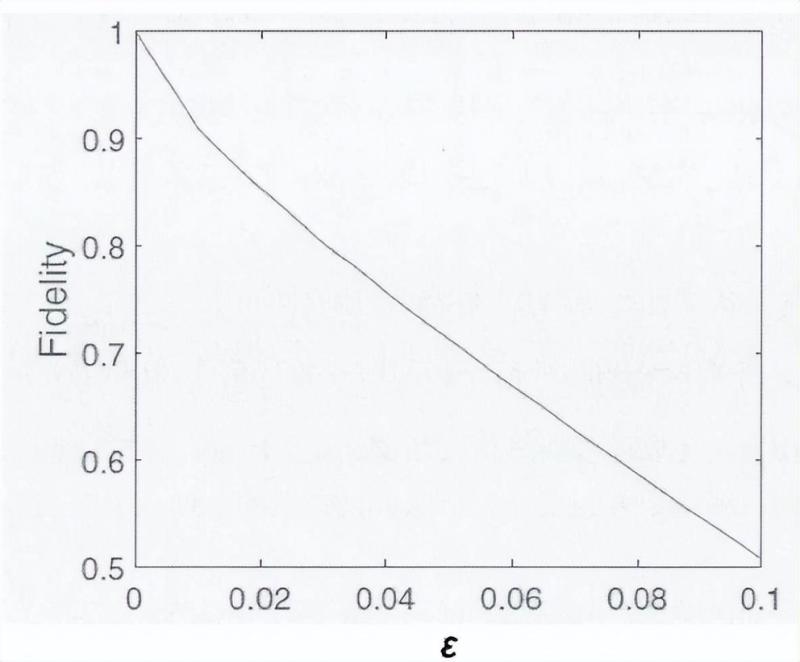
，／＾尝试过将三方关系去掉，只保留至多两方的观测结果，理想情况下保真度的值会降到30%以下，用边际信息测试多体量子态均是通过量子关联的期望值来实现的，是否存在有效Bell不等式实现对整体目标的量子态。

基于边际信息Bell不等式的自测试

Bell不等式是探究量子非局域性的有利工具，然而，与多体量子的相关Bell不等式的结构中会包含有所有方测量的联合期望值，这使得实验实现和统计的时候不易操作。

研究多体量子系统中，是否存在容易测量或者只用较少观测量就可以实现Bell非局域的不等式，因此对每方各有两个测量时N=3,4,5的量子比特的系统中，构造对称的且只包含一方和两方关联的不等式。

并证明了这样的不等式的经典界可以被一些确定的量子态违背，从而实现非局域的认证，我们将主要针对N=3量子系统的至多包含两方关联的平移不变的Bell不等式进行研究，证明其最大量子违背值可以唯一地认证一个3-qubit的纠缠态，而且自测试方案具有鲁棒性。

三方的Bell不等式表示如下：

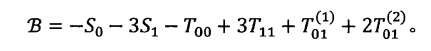
注意的是这个不等式是平移不变量，而不是轮转不变量，因为每方只有两个测量，所以可以考虑成投影测量，假设测量为：

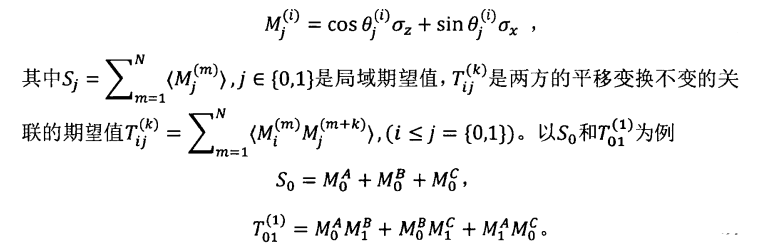
此不等式的最大经典界为９，而最大的量子界为10.02，但是最大量子界对应的目标态并不是常见的W态或者GHZ态，W态可以违背的最大量子界仅为9.85，但是它的最优量子策略可以通过自测试的方案得以验证。

三量子比特的纠缠态可以由上述只包含一方和两方关联关系的Bell不等式的最大违背值实现自测试，理想的swap线路图需要用不可信的测量代替σx和σz的操作。

为了实现这样的构造，首先我们分别把两个测量做一个X-Z平面的旋转μ=π/2-θ1角度，使得M1旋转到Ｘ方向，相应的Ｕ操作为：

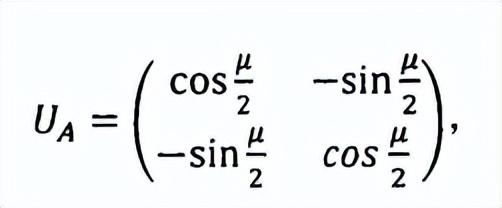
这里的目标态也要做相应的酉变换，而对应测量结果的统计值为：

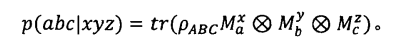
因此，当前的目标态和测量相差一个局域酉操作，但是这并不影响结论的成立，经过酉操作之后的两个测量不会改变彼此的相对夹角，每方第一个测量M0依然不是Z。

实际上，我们需要一个Z测量，为了解决这一问题，增加局域矩阵，主要思想是每方引进一个新的测量M2，新的测量M2需要用不可信的测量M0和M1约束，这里我们增加一个关于M2的局域矩阵，并满足：

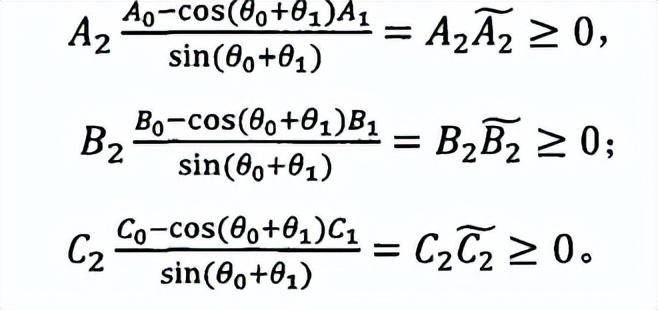
这里的局域矩阵使用2×2的小矩阵，具体地可以表示为矩阵：

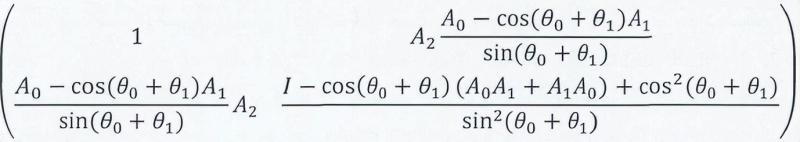
必须是厄米的和半正定的，需要指出的是局域矩阵并不是SDP矩阵的约束条件，而是对辅助的不信的测量算子的限制。

通过运行88×88的NPA矩阵和半正定规划，当测量结果是量子违背值时，保真度的变化可以由下图给出。

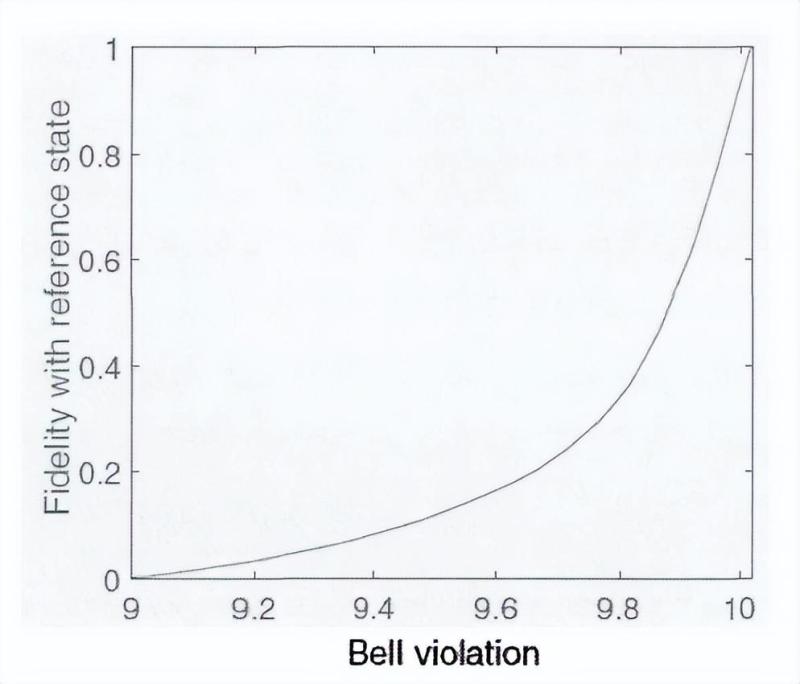
ｌａｔ除了W=3时的情况，我们的方法依然适用于N=4,5。

多体纠缠态的很多信息都可以编码到了它的部分态中，这个理论同时在纠缠理论和自由度认证中是成立的，给出了在设备无关框架下的相关结果。

利用swap方法以及相关的NPA层析和半正定规划，对3-qubit的W态、广义含有参数的W态和4-qubit的W态进行研究，分析了每方各持有三个测量时，利用观测边际概率信息的自测试整体量子态的结果。

并展示了统计结果理想情以及存在噪声时的保真度的随误差变化的曲线，此外，我们还研究了仅含有边际信息的Bell不等式对一类特殊的3-qubit纠缠态的自测试结果。

证明了其最大量子违背值可以唯一的认证最优的量子策略所对应的量子态和测量，并对任意测量到的Bell不等式的量子违背值给出了设备中的态与目标态之间保真度的界。

笔者观点

笔者认为，通过解析和数值两种不同的自测试方法，不仅可以对W态和GHZ态的叠加形式的纠缠态进行分析，而且可以实现保真度较高而且抗噪声的自测试，帮助量子计算、量子通信及其他相关领域的探索和开拓。

随着相关技术的发展，在未来需要进一步完善和拓展这些方法，以此来提高其适用性和鲁棒性，从而推动量子信息领域的发展和进步。